自编码器Auto Encoder
自编码器通用架构
自编码器概念最初被提出是基于对数据降维的目的,我们希望能够从原始特征$x$中,通过筛选、组合、变换等方式获得包含原始丰富信息的低维特征表示$e(x)$,通常$|e(x)|\ll|x|$,这种学习方式也称为表征学习Represent Learning。通俗的去思考,我们没有办法像监督学习那样对不同特征提前设定低维表征,这就需要一种自监督方法去发现原始特征之间的关系。表征学习的思路有很多种,这里我们沿着一类基于Encoder-Decoder架构的降维方法展开。这种架构利用编码器将原始特征降维获得低维编码,然后再利用解码器将低维编码重构。这相当于构造了一个自监督学习任务,学习目标是希望重构的结果与原始输入尽可能相同。这里的低维编码我们可以称为信息瓶颈,原始特征的重要信息可以经过信息瓶颈被重构。
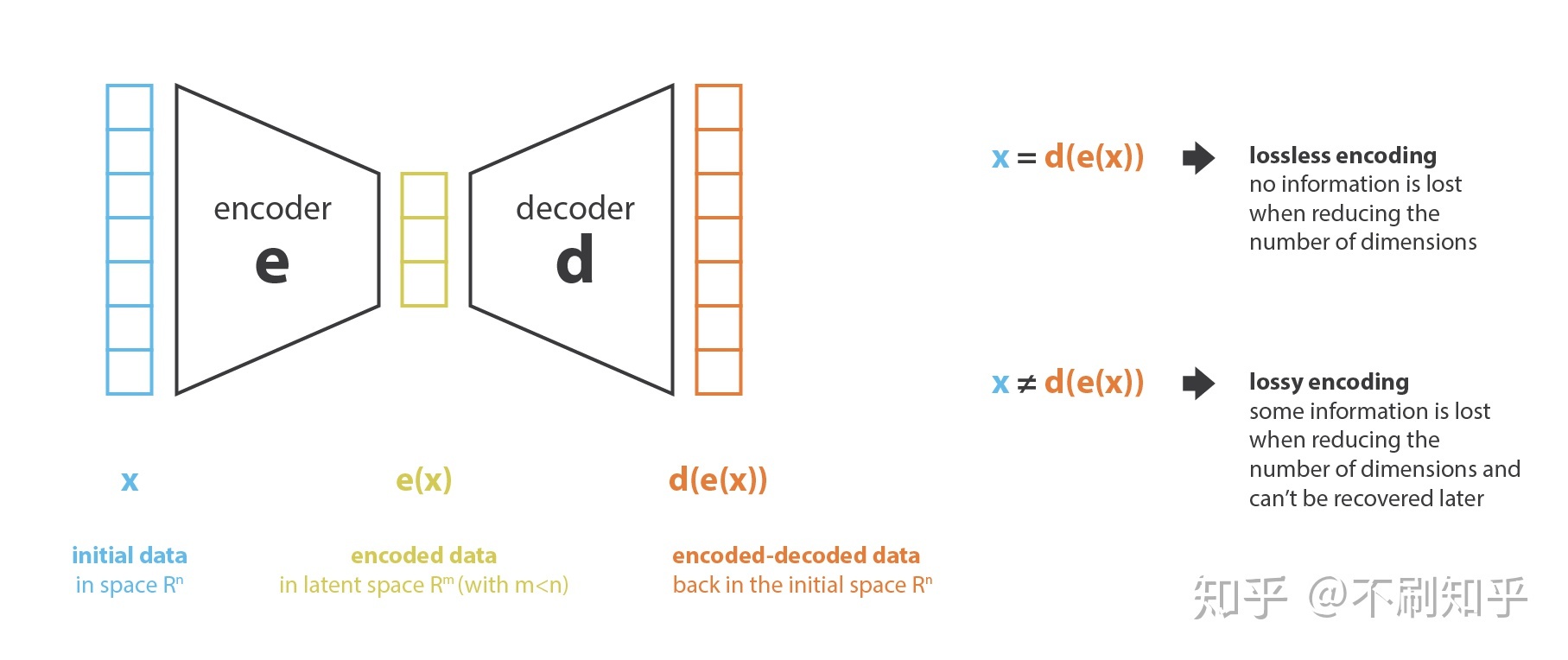
广泛的,降维问题可以被如下表示:
$$ e,d = \mathop{\arg\min}_{(e,d)\in E\times D}Loss(x,d(e(x))) $$
PCA降维
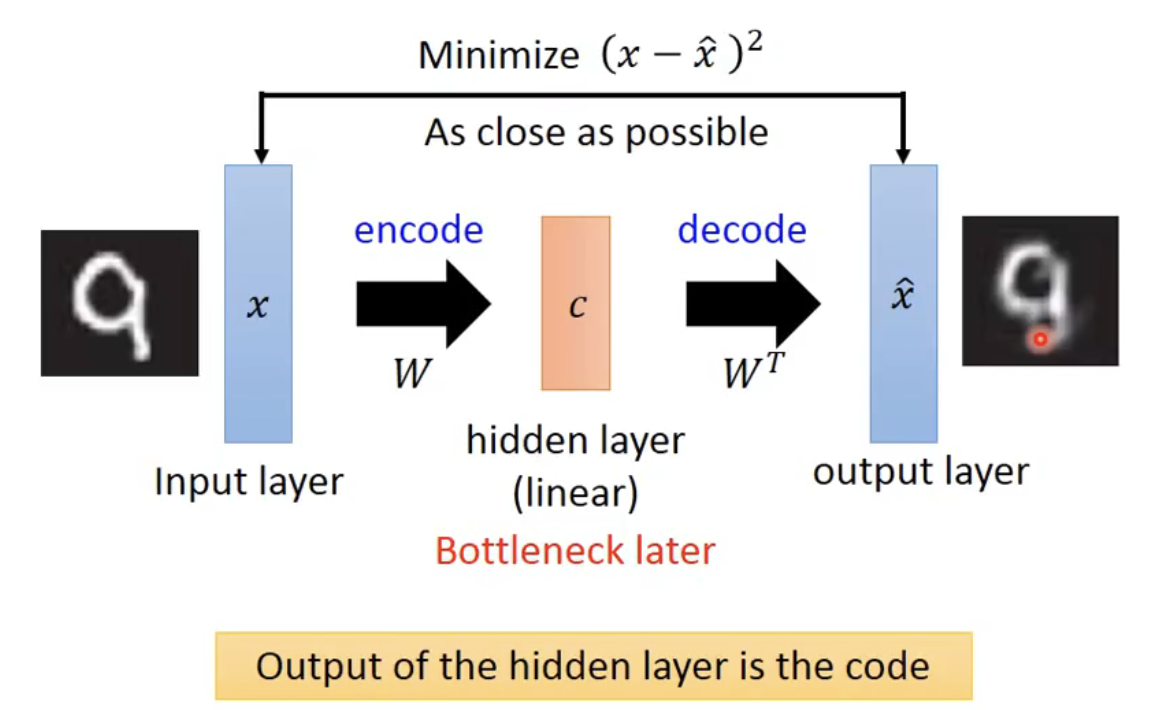
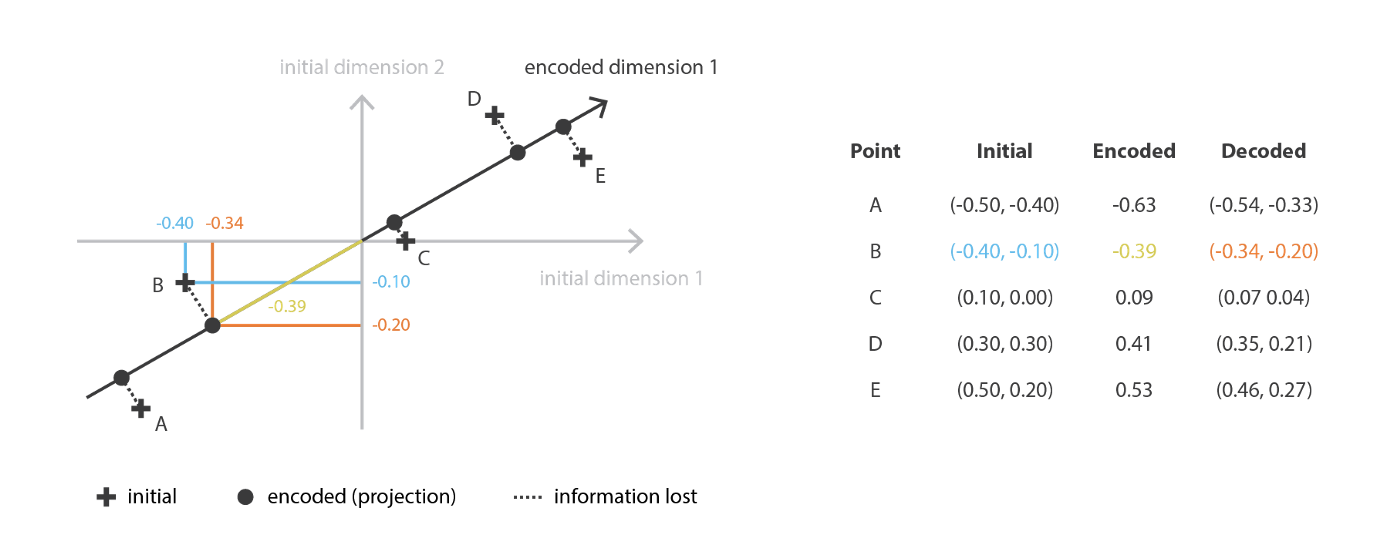
提到降维,很多人首先想到的应该是著名的PCA(主成成分分析),其主要原理是基于奇异值分解SVD分析主要特征,对原始特征作线性组合来投影到低维表示空间中。关于PCA的具体原理不多描述,但其主要过程可以被套入自编码器的框架当中,如下图所示。PCA中的编码器、解码器即为映射矩阵$W$与其转置$W^T$
Deep AutoEncoder
自编码器的关键在于编码器和解码器的映射关系。由此,我们考虑直接用神经网络强大的拟合能力去构造编解码器,在每次迭代中将解码器的输出与原始输入作比较,通过反向传播更新网络权重。
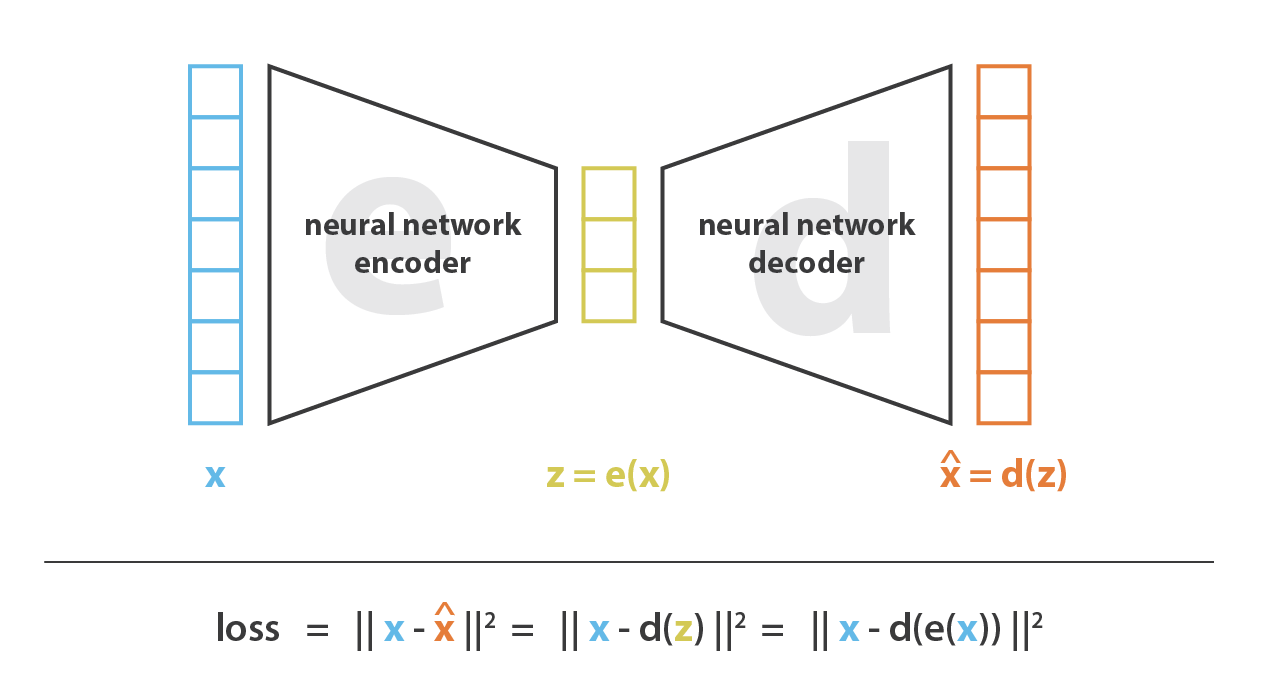
这个想法是Hinton在06年《Science》中提出(原文还释放了当时的代码)。值得一提的是,在那时Hinton就指出可以利用这种自编码器的架构,构建无监督任务去做pre-training,然后在真实数据上fine-tuning。所以本质上,预训练的思想就是构建合适的无监督任务(most important)来把模型参数作有效初始化,然后在有监督任务上用很少的成本微调参数,就可以获得很好的效果。不妨回顾当时的摘要:
High-dimensional data can be converted to low-dimensional codes by training a multilayer neural network with a small central layer to reconstruct high-dimensional input vectors. Gradient descent can be used for fine-tuning the weights in such “autoencoder” networks, but this works well only if the initial weights are close to a good solution. We describe an effective way of initializing the weights that allows deep autoencoder networks to learn low-dimensional codes that work much better than principal components analysis as a tool to reduce the dimensionality of data.
神经网络相较于PCA的最大优势在于其对特征的映射可以是非线性变换,这是矩阵变化无法实现的。换句话说,如果我们采用简单的网络且没有非线性变化(无激活函数),神经网络是可以模拟PCA的线性变换效果的。理论上,深度非线性神经网络可以将特征降维到足够小,并无损重构低维特征。在Hinton论文中,对于MINST数据集,可将每张图像的784维特征压缩到30维并清晰地重构,这在当时是非常难得的。
然而,我们并不能将信息瓶颈无限减小。因为更低维的编码虽然能被能力强大的解码器重构,但此时的解码器更多的是对数据编码的死记硬背,此时的中间编码不可避免的丢失了很多重要信息,如下图所示。左侧的一维降维使得只保留了是否生物性的信息,右侧的二维区分了生物性和飞行能力两个维度。过低维度的隐空间中缺乏可解释和可利用的结构(缺乏规则性,lack of regularity).由此,降维的目的并非信息熵越低越好,而是希望在减少维数的同时将数据主要的结构信息保留在简化的表示中。出于这两个原因,必须根据降维的最终目的来仔细控制和调整隐空间的大小和自编码器的“深度”(深度定义压缩的程度和质量)
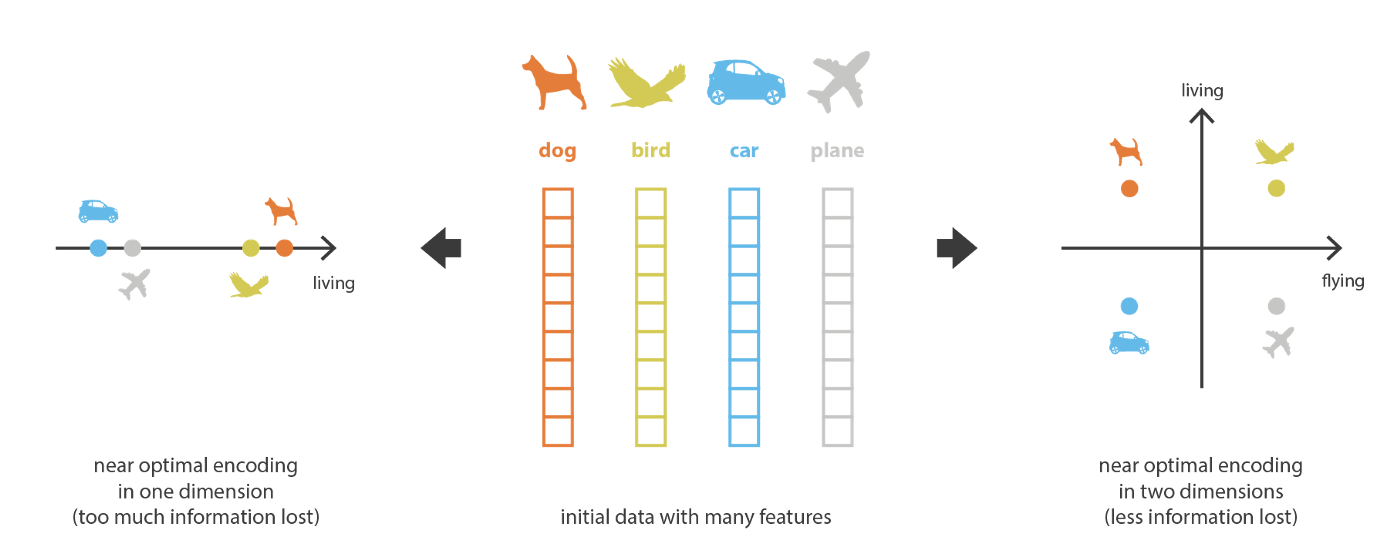
实际上,正如名字所述,自编码器出发点就是希望获得原始对象特征的低维表示,这种低维表示可以被应用到很多场景:
- 文本检索:获得document词向量并降维。获得query在降维空间中的表示,根据低维距离作文本检索
- 图像检索:不同于Pixel级别的距离表示,将query图像和所有待检索图像降维,利用低维空间中的距离评价图片相似度
- 模型权重的预训练
- ……
这些场景中我们的重点都在于编码器,而解码器只是作为训练过程中的辅助结构。但既然研究生成模型,我们的重点就需要关注解码器,因为他是生成目标的主力。但由于自编码器出发点的局限性,我们改造自编码器去生成图像是比较困难的,目前做的很好的工作就是接下来要讲的变分自编码器(VAE)。
(事实上个人观点,自编码器架构的局限性现在仍然限制着VAE的表达效果,毕竟他不是生来就去作生成任务的)
变分自编码器VAE
变分自编码器的重点在于解码器,目的在于构造一种生成模型,给定从特定分布中采样的向量编码,构造符合某种“形式”的输出,这里的“形式”是从解码器配合编码器从给定样本集中以自监督的方式学习到的。实际上,VAE是从《Auto-Encoding Variational Bayes》中被提出,文章本来的目的是提出一种称为Stochastic Gradient Variational Bayes的梯度估计方法,利用神经网络作变分推理,对变分推理的分布进行参数化。通俗的解释就是,我们希望能构造一个分布$q(x,\theta)$去拟合不能直接求解的分布$p(x|z)$,这里的$q(x,\theta)$我们直接用神经网络去构建。顺带着,作者提出了Variational Bayes Auto Encoding的算法,即VAE框架。这里贴出原文的主要Motivation:
How can we perform efficient inference and learning in directed probabilistic models, in the presence of continuous latent variables with intractable posterior distributions, and large datasets? We introduce a stochastic variational inference and learning algorithm that scales to large datasets and, under some mild differentiability conditions, even works in the intractable case.
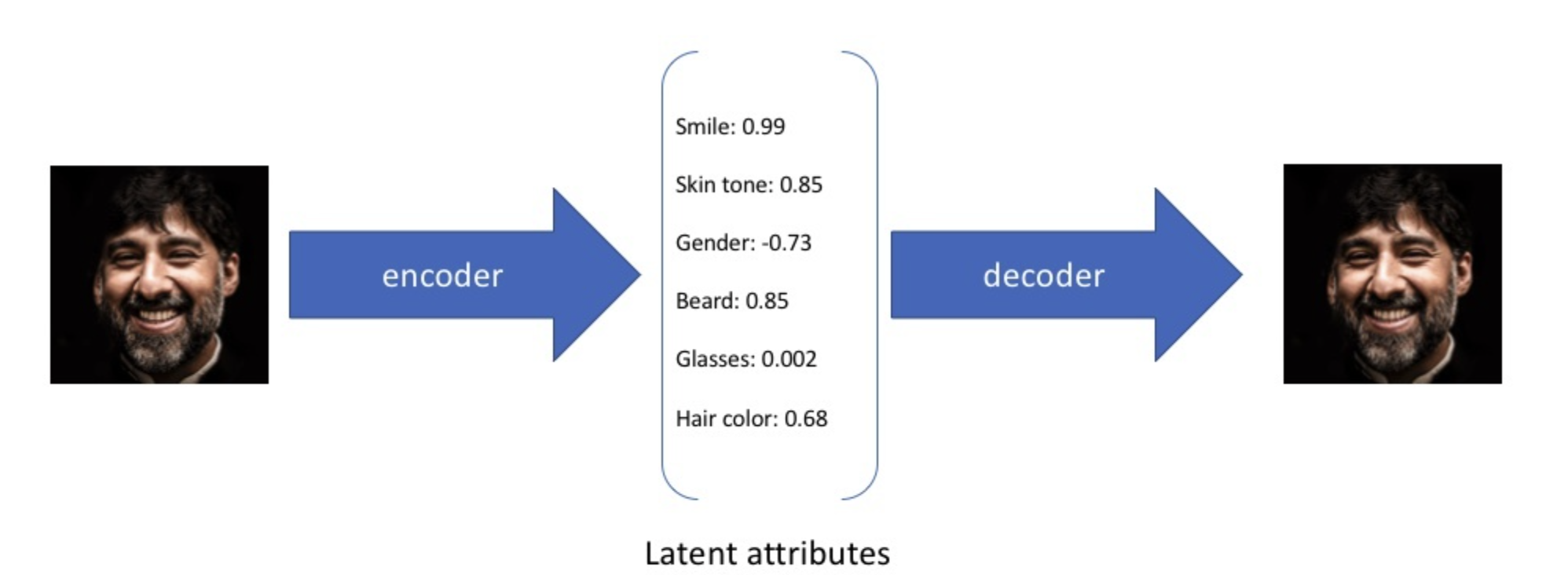
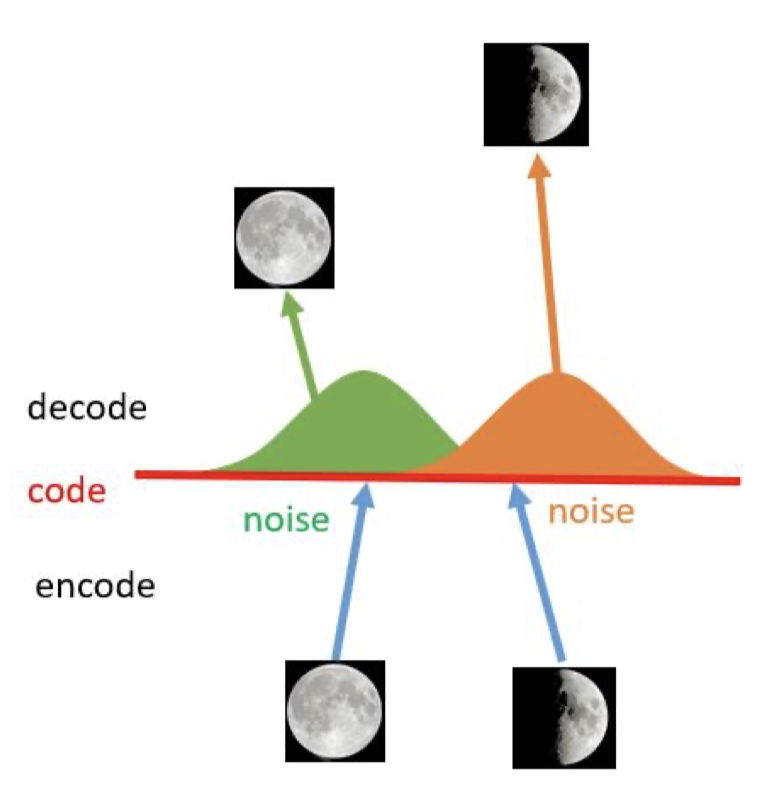
当然,VAE的结构出自于Auto Encoder,但是两者目标不同,我们不能类比着考虑,或者说,虽然Auto Encoder也有根据编码$z$生成结果的过程,却无法直接用来作为生成模型。原因在于,自编码器的学习目标学习到的编码,在隐向量空间上是过度拟合的,具体表现在相似输入的编码在隐向量空间中是离散的,不具备线性迁移的能力。或者说,编码器解码器是“硬性”地记住了不同编码,但编码与编码之间并没有密切的联系。
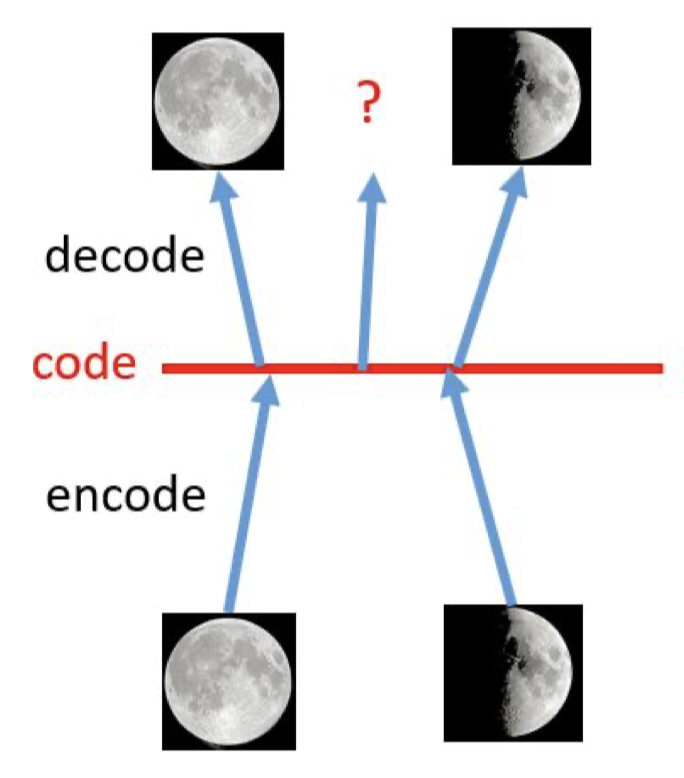
如上图所示,对于全月和半月的编码,解码器能够无损的获得原始图像。但如果我们从两个编码的线性区域中间采样,这里的中间编码解码器是无法生成有意义的结果的,即没有生成能力。归根结底,是由于自编码器的损失只取决于生成结果和原始数据的差异,不关心隐空间中的编码向量如何组织。想到这里,如果我们能将隐空间的编码规范化也作为学习的目标,也就可以让解码器对隐空间中的连续区域的采样进行解码,而不只是局限在离散编码点当中。通俗的理解,我们希望能够泛化对数据的编码空间,让其不过度拟合到特定的离散编码中,这就是编码规范化的过程。
要实现对编码的泛化,我们首先可以考虑对原始图像加入噪声,这样可以对让编码器对输入的编码聚集在某个区域当中,但这还不够充分。VAE的高明之处在于「用一个分布来表示对某一数据的编码」,这就实现了将原本离散的编码构造成为一种「连续编码」。以下是对这句话含义的解释。
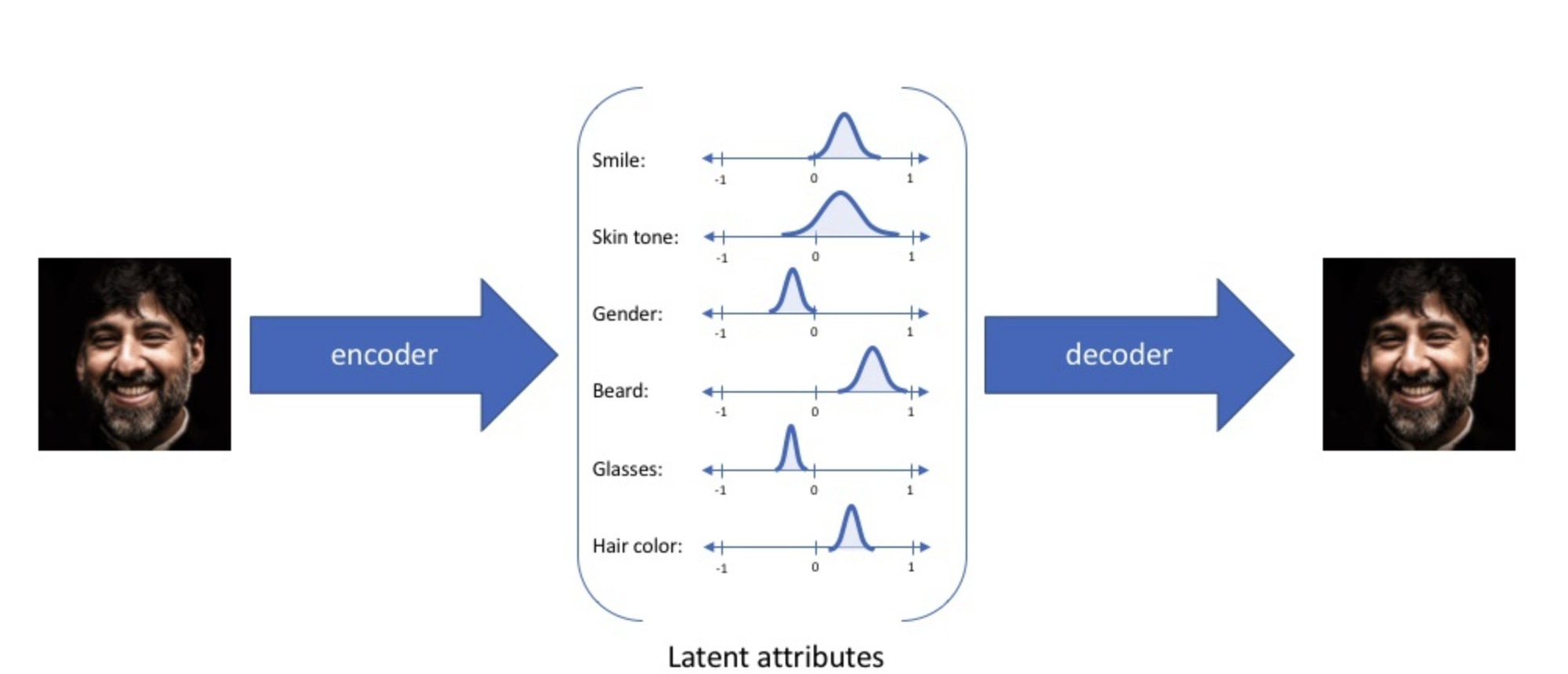
对于VAE作生成模型,我们希望的是能够从编码空间中随机采样的隐向量$z$都能够有一个近似的生成结果,而且越接近于原始图像的编码,其与原始图像的特征越相似。VAE做的就是将离散编码(如$z=[2,4,3,6]^T$)变成一种连续函数的形式(如$Z=\mathcal{N}(\mu,\sigma^2),\mu,\sigma^2 \subset \mathbb{R}^n$),如上图所示。有了编码分布后,我们从中随机采样来获得编码向量$z=rand(Z)$。理论上,从分布中采样得到的编码都可以包含原始数据的一些信息,而距离均值的位置,包含信息是最多的。这样做的的好处是在两个分布重合位置的编码,是包含两个数据的共同特征的,如此就实现了对于编码的连续型。VAE的训练经过正规化以避免过度拟合,并确保隐空间具有能够进行数据生成过程的良好属性。
如上图所示,通常,我们用正态分布来做编码。在实践中,要表达一个正态分布,我们需要有其均值$\mu$和方差$\sigma^2$,注意这里的$\mu,\sigma^2 \sub \mathbb{R}^n$都是多维变量。想到这里,我们就知道了VAE中的编码器实际的工作就是对输入数据构建其分布的均值和方差。注意,每个输入数据$x_i\in X$,都有专属对应的正态编码分布,从编码器的角度$\mu_i,\sigma_i^2 = e(x_i) \sub \mathbb{R}^n$,从输入数据$x_i$的角度,其专属分布$p(z|x_i)=\mathcal{N}(\mu_i,\sigma^2_i)$。所以,完整VAE的架构如下图所示。
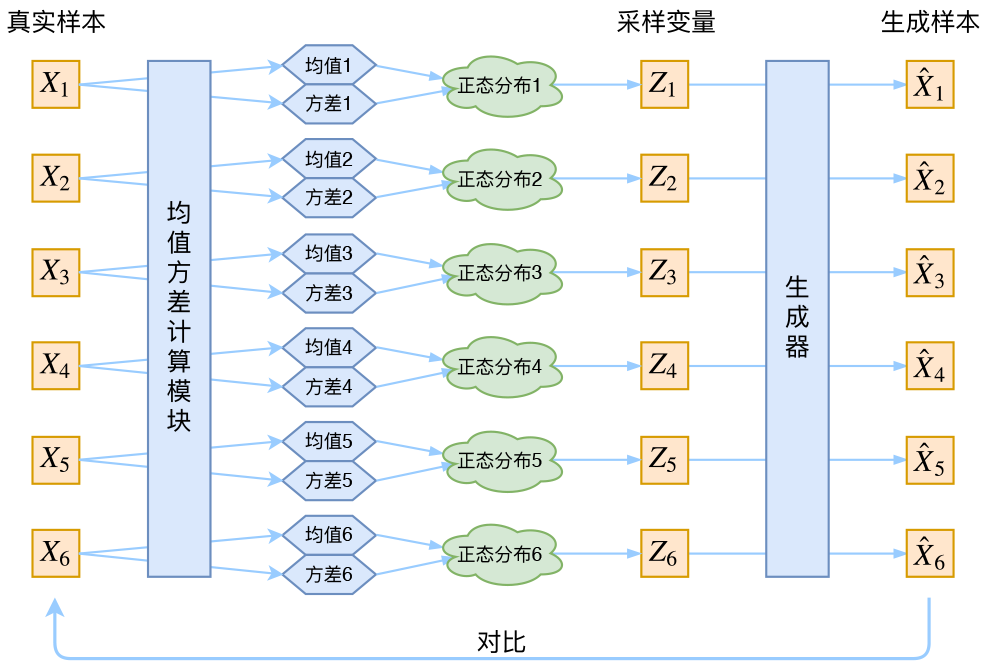
编码细节
知道了VAE对每个数据使用正态分布来编码,那问题来了,我们如何让模型去学习数据和分布之间的关系呢?从上面的分析我们可以得知,既然要用分布去编码,而编码的分布$p(z|x)$是正态分布(先验知识),那编码器可以直接输出属于该数据分布的两个参数:均值$\mu$和协方差矩阵$\sigma^2$。即我们可以构建两个神经网络:$\mu_i=f(x_i);\log \sigma_i^2=g(x_i)$来拟合两个参数。这里之所以拟合$\log \sigma^2_i$而非$\sigma_i^2$,是因为$\log \sigma^2_i$可正可负,而$\sigma_i^2$是正数需要加激活函数作特殊处理。从正态分布的角度看,拟合的均值和方差分别确保隐空间的局部和全局正则化(局部是由于方差控制,而全局是由于均值控制)
这样处理后,我们观察上图中的VAE架构可以发现,相比原始的Auto Encoder的不同点主要有两个:一是多加了一个编码输出(用来编码方差$\sigma^2$);二是编码$z$是从分布中采样得到的。这里让VAE实现生成能力的其实是第二点,因为$z$不是从Encoder直接获得的,我们希望从分布中采样得到的$z$经过生成器得到的输出$\hat{x_i}$能够和原始输入$x_i$尽量保持一致,采样的过程实际是增加**「噪声」**的过程(完整的编码$\hat{z}$为均值,采样后的$z$与$\hat{z}$存在偏移。这里我们先不考虑采样导致的误差backward困难问题),增加了重构的难度。但如上文所说,均值和方差能够确保隐编码空间的正则化,直白些就是方差可以控制噪声的强度,较小的方差可以让采样尽可能保持在均值附近。而方差又是由编码器的神经网络计算,所以「网络如果想尽可能保证重构效果,会倾向于尽可能减小噪声,网络会尽可能让方差为0。」这样的话,编码的分布也就没有随机性,不管怎么采样都会得到均值处的结果。这也就退化为基本的Auto Encoder了,方差编码也就不再起作用
该如何解决噪声退化问题呢,我们在学习目标上加入对编码器「正则化」的约束,让所有的编码分布都向「标准正态分布」看齐(至于如何想出来的我也很想知道)。这样就可以防止噪声为0,同时也保证了模型的生成能力。如何理解标准正态分布可以保证模型的生成能力?我们的目标是希望编码分布$p(z|x_i)$接近标准正态分布$\mathcal{N}(0,1)$,那么根据定义:
$$ p(z)=\sum_{x_i\in X}p(z|x_i)p(x_i)=\sum_{X_i\in X}\mathcal{N}(0,1)p(x_i)=\mathcal{N}(0,1)\sum_{x_i\in X}p(x_i) = \mathcal{N}(0,1) $$
这样,我们直接利用解码器生成结果时,可以从正态分布中随机采样$z=rand(p(z))$,任何编码$z$都可以生成有特定信息的结果。
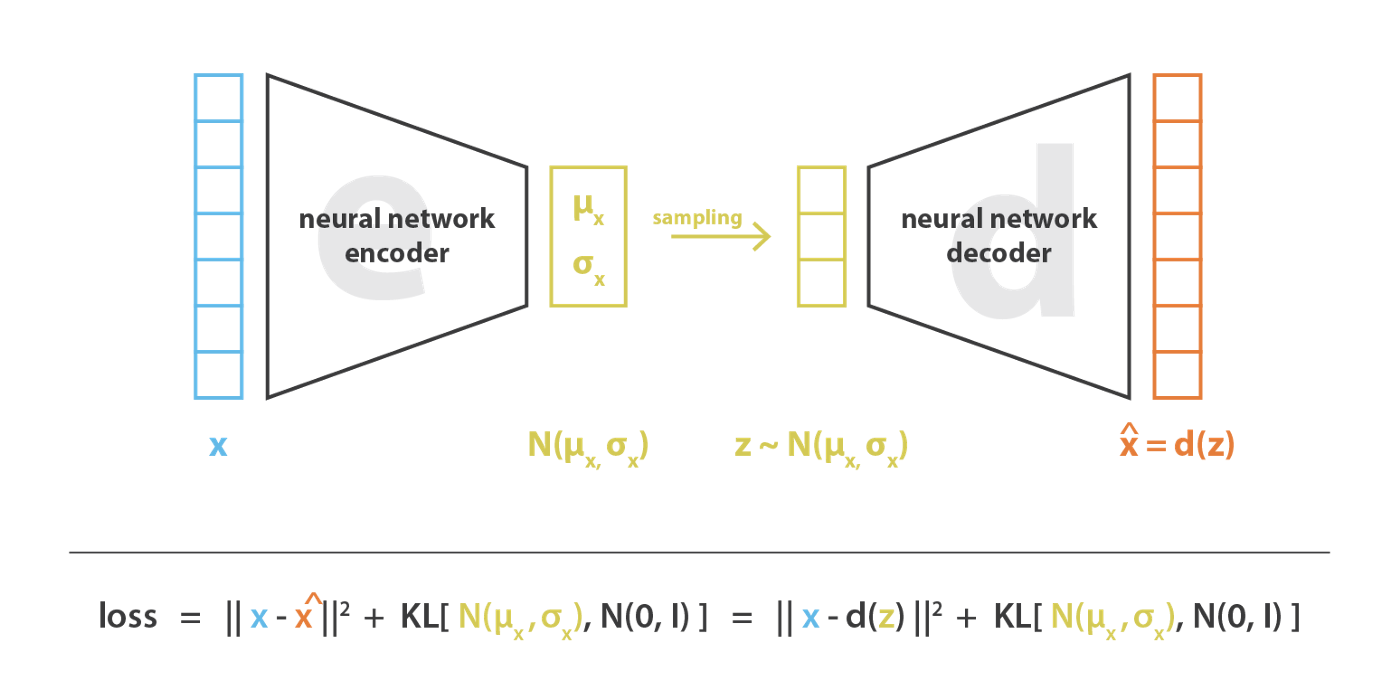
要使每个编码分布看齐正态分布,我们可以在损失函数中加入KL散度来衡量到正态分布的距离。编码分布$p(z|x_i)=\mathcal{N}(\mu_i,\sigma^2_i)$越接近正态分布$\mathcal{N}(0,1)$,KL散度越小。如此,如上图所示,VAE的学习目标包含两个部分:重构项$||x-\hat{x}||^2$,正则化项$KL(\mathcal{N}(\mu_i,\sigma^2_i),\mathcal{N}(0,1))$。前者用来优化编码-解码结构,后者用来规范编码空间
这里我们更为细致地思考一下为何要正则化,让编码分布看齐正态分布呢?
我们用编码均值和方差的方法构造正态编码分布,这种分布$p(z|x)$满足正态分布$\mathcal{N}(\mu,\sigma^2)$我们可以视为先验的,他并不能避免噪声退化问题。为了使生成过程成为可能,我们期望隐空间具有规则性,这可以通过两个主要属性表示:连续性(continuity,隐空间中的两个相邻点解码后不应呈现两个完全不同的内容)和完整性(completeness,针对给定的分布,从隐空间采样的点在解码后应提供“有意义”的内容)。连续型和完整性的实现需要不同样本$x$的编码分布尽可能接近,并且方差不能为0以保证采样的随机性(见下图)。正则化编码分布,我们可以防止模型在隐空间中的编码相互远离,并鼓励尽可能多的返回分布发生“重叠”,从而满足预期的连续性和完整性条件。
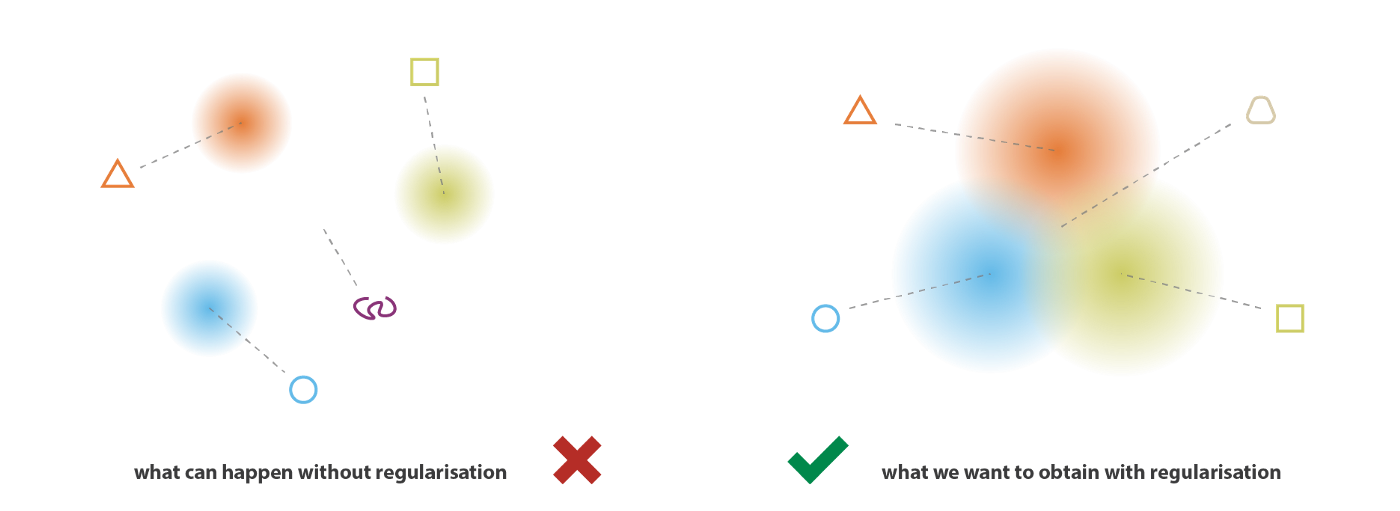
另一方面,对样本的重构误差有希望编码内容需要尽可能保留原始样本的信息,也就导致的编码空间的多样性。从这个角度看,VAE当中也是存在一种对抗的思想,只是比较隐晦,并且是共同进化。宏观角度展开这种对抗思想,即当Decoder训练的不够充分,重构Loss更大,网络会降低噪声(KL loss增大,这里理解始终$\sigma^2 <1$),采样的$z$更接近原始数据均值,包含更多原始信息,以方便更好的重构;反之当Decoder训练的很好,KL Loss更大,就需要增大噪声(降低KL Loss),方差更接近1,采样区域也就更加广泛,似的重构更加困难,此时又需要Decoder增强其重构能力。
说了这么些,总结一下VAE:VAE是将输入编码为分布而不是点的自编码器,并且其隐空间结构通过将编码器返回的分布约束为接近标准正态分布而得以规范化。
VAE的数学由来
我们前面说到,VAE在原论文中是以一个配角身份被提出的,但能发展到现在也足以说明其理论有效性。接下来我们就从原始论文的角度对VAE作一番推导。
文章的目标是要解决有向概率图模型的有效推理,在大型数据集中,概率图往往存在由于参数众多而难以解决的后验分布。同样针对自编码问题,给定观测到的数据样本集$X$,我们希望给定样本$x\in X$的条件下推理出其编码$z$的后验分布$p(z|x)$。
作为先验知识,我们假设编码分布$p(z)$属于正态分布,那么这个$p(z|x)$即为编码器Encoder,要对其求解,我们可以考虑贝叶斯公式: $$ p(z|x)=\frac{p(x|z)p(z)}{p(x)} $$ 然而贝叶斯公式中,我们无法直接计算分母$p(x)$和$p(x|z)$,因为全概率公式$p(x)=\int p(x|u)p(u)du$,我们无法列举所有$u$。这种情况下,我们还有两种思路求$p(z|x)$:
- 蒙特卡洛取样 (这里不看)
- 变分推理
变分推理的原理很好理解,原分布$p(z|x)$无法计算,我们就构造一个新的可解的分布$q(z|x)$去拟合,使两个分布尽可能接近。评价分布的距离就用到了KL散度。
那么现在,我们就用分布$q(z|x)$去拟合原分布$p(z|x)$。注意到这里的$x$指的是从样本集中选出的某个样本,我们拟合的目标是专属与该样本的分布。作为先验知识,我们假设样本的编码符合正态分布$q(z|x)=\mathcal{N}(\mu_x,\sigma^2_x)$。这样,我们的目标就变成了给定样本$x$拟合其编码分布的两个参数$\mu_x,\sigma^2_x$。如何拟合?神经网络!用$f(x),g(x)$分别拟合$\mu,\sigma^2$(或者如上文提到的$\log \sigma^2$)即$q(z|x)=\mathcal{N}(f(x),g(x))$。
我们想让$q(z|x)与p(z|x)$尽可能接近,就是要让两分布的KL散度尽可能小。换句话说,我们希望找到最优 $f^*,g^*$ ,使得
$$ (f^*,g^*)=\arg \min_{f,g}KL(q(z|x)||p(z|x)) $$
推导之前我们回忆一下,我们目前要做编码$p(z|x)$,没法直接算就用$q(z|x)$去拟合。我们目前还没提到VAE哦。ok,开始推导:
$$ KL(q(z|x)||p(z|x))=\int q(z|x)\log \frac{q(z|x)}{p(z|x)}dz =\int q(z|x)\log \frac{q(z|x)}{\frac{p(x|z)p(z)}{p(x)}}dz =\int q(z|x)\log q(z|x) \frac{p(x)}{p(x|z)p(z)}dz $$
根据log对式展开:
$$ KL(q(z|x)||p(z|x))=\int q(z|x)\log q(z|x)dz+\int q(z|x)\log p(x)dz-\int q(z|x)\log p(x|z)dz-\int q(z|x)\log p(z)dz =\log p(x)+\int q(z|x)\log \frac{q(z|x)}{p(z)}dz-\int q(z|x)\log p(x|z)dz $$
好戏来了:
$$ KL(q(z|x)||p(z||x))=\int q(z|x)\log \frac{q(z|x)}{p(z)}dz-\int q(z|x)\log p(x|z)dz+\log p(x) =KL(q(z|x)||p(z))-\mathbb{E}_{z\sim q(z|x)}[\log(p(x|z))]+\log p(x) $$
这个公式就厉害了,让我们好好分析一通。整体来看,我们希望整个式子去最小值,那就是第一项KL散度越小越好,第二项期望越大越好。至于第三项,虽然$p(x)$我们不知道,但给定所有样本,那他就是一个常数,可以不管。
继续分析。第一项KL散度,他代表了我们假设的后验分布$q(z|x)$与先验分布$p(z)$的距离,原文中$p(z)$被假设为「标准正态分布」,原文解释如下:
The key is to notice that any distribution in $d$ dimensions can be generated by taking a set of d variables that are normally distributed and mapping them through a sufficiently complicated function.
第二项期望,他本质是说明了这样一件事:对于我们用来拟合的分布$q(z|x)$,给定样本$x$生成的编码分布中,我们采样出$z$,用这个$z$重构的结果$\hat{x}$应该与样本尽可能一致。其实我们写成下式更方便理解一些: $$ \mathbb{E}_{z\sim q(z|x)}[\log(p(\hat{x}|z))] $$ 公式(10)告诉我们,要使假设的分布$q(z|x)$与后验分布$p(z|x)$尽可能一致,一方面需要让$q(z|x)$接近先验分布$p(z)$。更重要的,我们还需要对采样的$z$作重构操作,让重构后的结果$\hat{x}$极可能与样本$x$一致。既然涉及到重构操作,那我们还得引入一个神经网络(或者别的东西)。如此一来就回归到了Auto Encoder的架构当中。
所以我们简单总结一下,VAE原始的出发点就是希望能用一个分布去做编码,但这个分布不能直接求解,就需要用到变分推理,用神经网络去拟合近似的分布,这也是V(Variational)的含义。而在优化这个拟合分布过程中,我们需要借助对编码采样的重构过程去优化拟合函数,所以引入了解码器,至此,形成了通用的AE架构。
回顾VAE的Loss函数:

再继续分析下去,优化项中的期望就代表了生成结果和样本的距离,我们用$||x-\hat{x}||^2$衡量;优化项中的$KL(q(z|x)||p(z))$,由于先验$p(z)$属于标准整体分布,是有具体解析式的,而$q(z|x)$我们也假设为一种正态分布,其包含的参数——方差和均值我们分别用两个神经网络来拟合:$\mu_x=f(x),\sigma_x^2=g(x)$,我们也可以写出具体的包含$g,f$的解析式,对KL项可以优化为: $$ KL(\mathcal{N}(\mu,\sigma^2)||\mathcal{N}(0,1)=\frac{1}{2}(-\log \sigma^2 + \mu^2+\sigma^2-1) $$ 最终,就获得了VAE中的优化函数: $$ Loss =||x-\hat{x}||^2+\frac{1}{2}(-\log \sigma^2 + \mu^2+\sigma^2-1) $$